Assume the charge initially on spheres A and B is
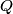 . After sphere C is touched to sphere A, the charges on sphere A is . After sphere C is touched to sphere A, the charges on sphere A is 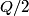 , the charge on sphere B is , the charge on sphere B is 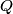 , and the charge on sphere C is , and the charge on sphere C is 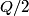 . After sphere C is touched to sphere B, the charge on sphere A is . After sphere C is touched to sphere B, the charge on sphere A is 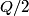 , the charge on sphere B is , the charge on sphere B is 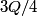 and the charge on sphere C is and the charge on sphere C is 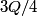 . The force between spheres A and B is given by Coulomb's law . The force between spheres A and B is given by Coulomb's law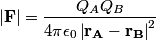 So, the initial force is 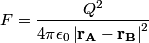 and the final force is 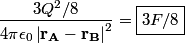 Therefore, answer (D) is correct. |